News Story
Flocks and Form
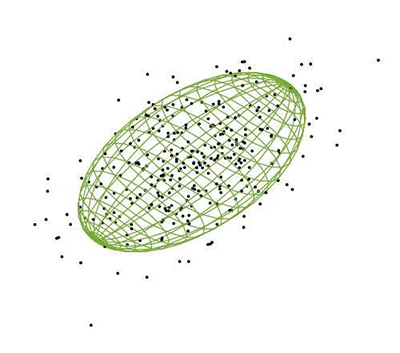
Ensemble inertia tensor of a collective (point cloud) visualized as an ellipsoid located at the center of mass (Figure 1 of paper – copyright Royal Society)
Picture a flock of birds in the sky – a migrating cohort of geese, a patch of swifts, or a murmuration of starlings. You notice patterns and changing forms – a 1 dimensional undulating rope of geese, or a 3D deformable solid suggested by a point cloud of starlings. The imagined solid may rotate as a whole and change orientation, scale, density, or transform from an ellipsoid to something more elaborate in the blink of an eye. Can one provide effective descriptions of form, and suggest ways to capture the essential kinematic modes that govern transformations of form?
Questions along similar lines had been posed and explored by chemists. Molecules of matter display symmetries in the configuration of individual atoms held together by chemical bonds. For instance, each molecule of the greenhouse gas Methane (CH4) has four Hydrogen atoms occupying the vertices of a platonic solid, the tetrahedron, and a Carbon atom located at the dead center. But this is a nominal structure which is subject to vibrations (hence change of shape) and rigid motions, as thermal energy is absorbed from and re-emitted to the environment—the domain of infra-red molecular spectroscopy. Quantum mechanics governs the frequencies of modes of vibration; in general there are 3n-6 such modes in a molecule made up of n atoms. Vibration co-exists with rotation and attempts at decoupling them failed, and as we now know thanks to the insights of mathematician Alain Guichardet, for reasons that lie in the geometry of fiber bundles (spaces with a certain local product structure).
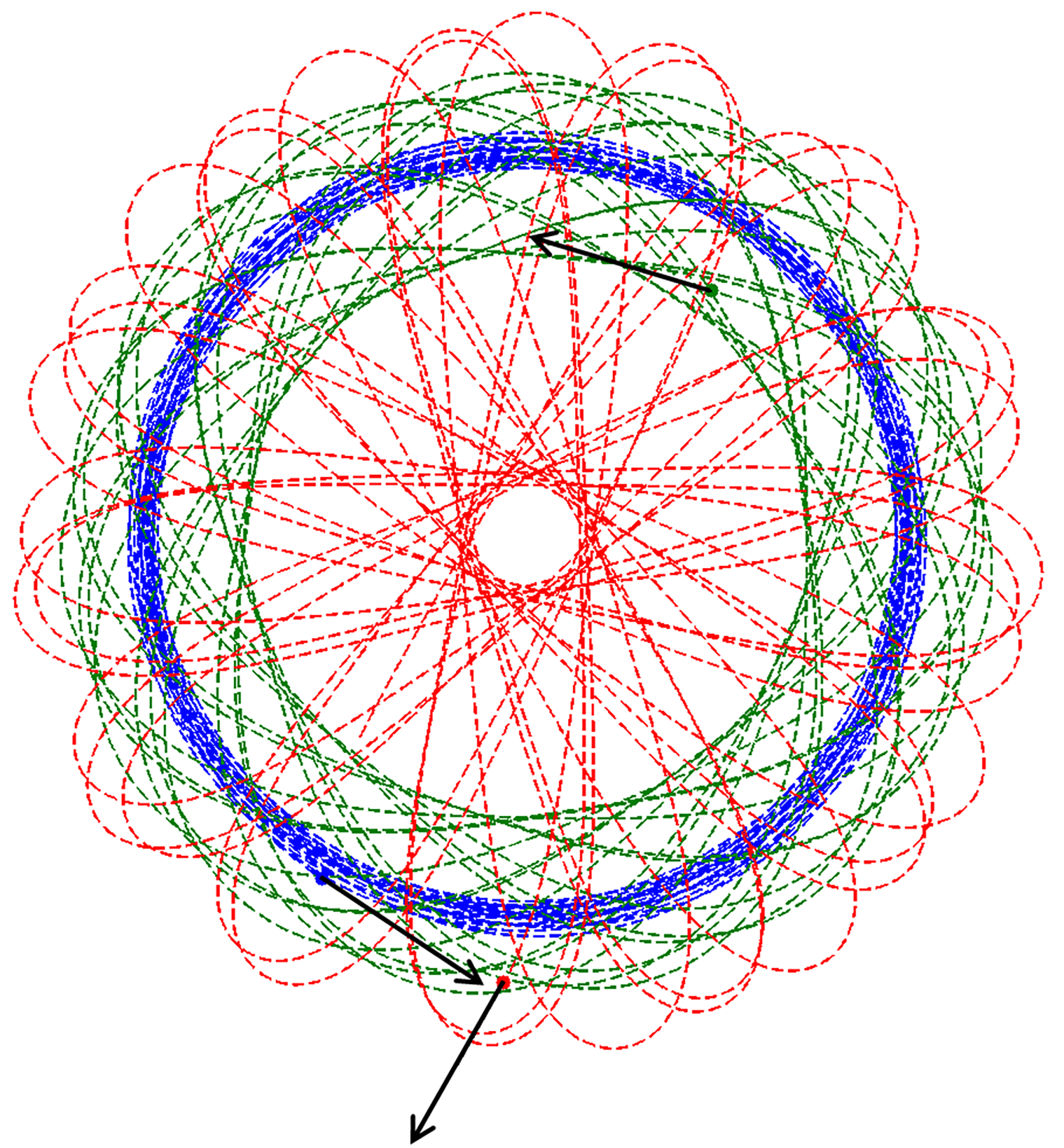
One difficulty with the chemists’ tools lies in the high dimension of the shape space of a complex molecule, thus rendering them unwieldy for tackling large flocks. In "Geometric decompositions of collective motion," appearing on April 26 in the Proceedings of the Royal Society A, the authors devise a new fiber bundle structure to describe the changing forms of flocks and underlying kinematic modes. The journal website includes supplementary material that provides details on how the concept of ensemble inertia tensor described by just 6 parameters, is the key to the new structure. Under certain generic conditions, flock data can be factored into such a tensor and coordinates on a Stiefel manifold, a space that has played an important role in various areas of mathematics and applied science. The modes are arrived at in a principled manner via modern tools from the field of differential geometry. Using notions of energy attributed to various types of collective movement, the authors shed new light on data obtained by previous researchers from small flocks of pigeons in free flight over large distances.
The paper was written by HHMI Janelia Research Campus Scientist Matteo Mischiati (EE Ph.D. 2011), and University of Maryland Professor P. S. Krishnaprasad (Electrical and Computer Engineering/Institute for Systems Research). The top-down approach of this paper complements their earlier collaboration based on the abstraction of agents in a collective as self-steering particles interacting according to strategies such as mutual motion camouflage.
The mathematics of fiber bundles underlying this paper has roots in twentieth century efforts to build new geometric foundations for physics, guided by the pioneers Elie Cartan and Charles Ehresmann. The authors use the kinetic energy quadratic form to construct velocity splittings, or connections in the sense of Ehresmann, that pave the way for computing kinematic modes of a flocking event. There are other threads that suggest steps to exploit the analytical tools of this paper in synthesizing algorithms for motion planning for collectives of robots. A different concern for the biologist may be posed:
Just as spectroscopic read-outs provide chemical signatures of molecules in a sample being interrogated, could one speculate that energy splits amongst kinematic modes in the course of a flocking event yield some tell-tale signatures of the event? Further experience in analyzing large flock data may help answer this question.
Published April 26, 2017