News Story
New quantum framework yields generalizations of bosonic ‘cat codes’
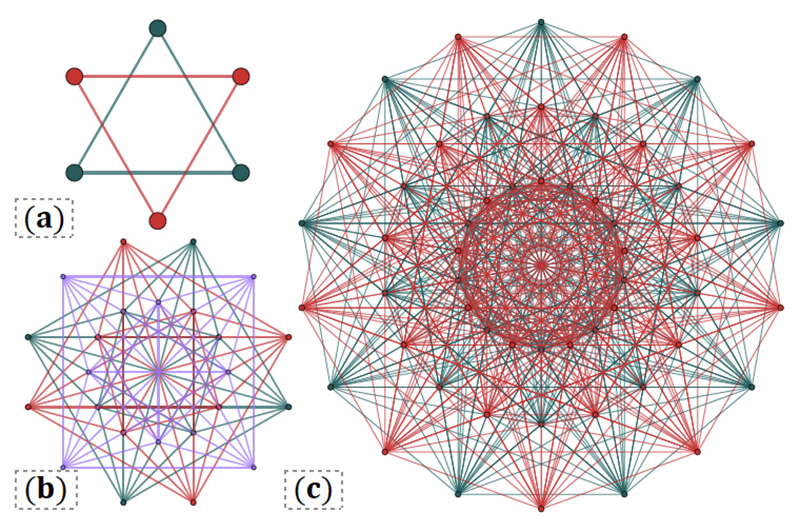
Figure 1 from the paper. Quantum spherical codewords are quantum superpositions of constellations on a sphere. Codeword constellations can form the vertices of a polytope and unite to form a code polytope compound. Projections of polytope compounds are shown for the (a) cat, (b) Möbius-Kantor, and (c) Hessian quantum spherical codes, with codeword constellation points colored either green, red, or purple.
Bosonic (a.k.a. oscillator) codes offer alternative qubit blueprints that are compatible with continuous-variable (CV) quantum platforms and that can reduce overhead by offering an extra layer of protection. Qubits defined on a few bosonic modes or more exotic spaces are likely to prove useful as control of quantum systems improves, but the field remains relatively under-explored in part because structures and intuition from qubit-based coding theory need not apply.
In a new paper, “Quantum Spherical Codes,” Professor Alexander Barg (ECE/ISR), Physics graduate students Shubham P. Jain and Joseph T. Iosue, and Adjunct Assistant Professor Victor V. Albert (Physics) develop a framework that yields generalizations of a class of bosonic codes called “cat codes” and unifies such codes with several others. Jain, Iosue and Albert are part of the NIST/UMD Joint Center for Quantum Information and Computer Science, led by UMIACS. Iosue is also part of the Physics Dept.-led NIST/UMD Joint Quantum Institute.
The researchers’ key observation is that all such codes are particular instances of quantum versions of spherical codes, a family well known in classical coding theory. They overview the framework and demonstrate its utility with several new multimode cat codes. A rigorous study of general features will be included in a companion follow-up work.
They introduce a framework for constructing quantum analogs of the classical spherical codes, encapsulating several physically relevant quantum coding schemes for bosonic, spin, and molecular systems. This framework is applied to obtain multimode cat codes based on polytopes, CSS qubit codes, and classical codes—some of which outperform previous cat-code constructions.
There are many other ways of constructing spherical codes, e.g., as group-orbit codes, as spherical embeddings of association schemes, through computer searches, and many others, as well as ways of constructing spherical designs. The authors anticipate their work will pave the way for many novel, well-protected, and experimentally feasible logical qubits.
Published February 28, 2023








