Narayan is PI for NSF information-theoretic signal processing sampling research grant

Professor Prakash Narayan (ECE/ISR) is the Principal Investigator for a three-year, $475K National Science Foundation Communication and Information Foundations grant for “Reconstructing Multiple Sources by Spatial Sampling and Compression.”

Abstract
The mathematics of signal processing underlies much of the modern digital world today. Digital signal processing relies on a technique called sampling, that allows information to be gathered about the underlying signal using a subset of samples from the signal, and information theory is used to describe fundamental principles of sampling. This project takes an information theoretic approach to develop fundamental principles that govern sampling of a small subset of a much larger set of correlated signals and processing them efficiently in order to reconstruct accurately a desired larger group of signals. These principles will be useful in myriad applications, for instance, in: potential smart homes with multiple networked smart sensor devices operating under transmitter power and channel bandwidth limitations; aerial surveillance systems for monitoring city traffic patterns or forest covers in which sources of information far outnumber the unmanned aerial vehicles or satellites that can be deployed; computer vision systems where data obtained from a limited camera scan and sensing must be interpolated to form a larger picture; and spotting trends in large social networks by polling small groups and gathering contextual data.

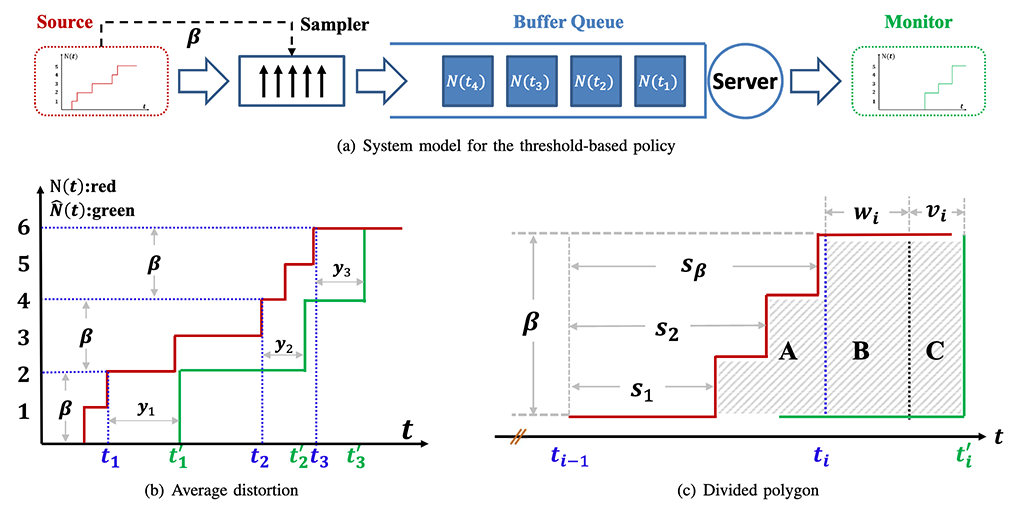
The tasks the signal processing system is to perform include: limited random sampling of spatially correlated time-signals; compress the samples for efficient channel transmission or storage; and recover, by decompression, a desired larger subset of the original signals with high accuracy. Optimality of such signal processing relies crucially on methods for estimating the unknown statistical behavior of the joint signals. A common framework will be developed for analyzing interwoven concepts of spatial signal sampling, estimation of joint signal statistics, lossy compression and signal reconstruction. New information theoretic formulations and approaches will be developed in this project with the objective of understanding basic underlying principles that will lead to implementable signal processing algorithms. The technical approach involves the development of a theory for signal processing with three main distinguishing features: (i) coordinated random spatial sampling of subsets of multiple correlated signals; (ii) statistical learning of unknown signal probability distributions; and (iii) universal rate-efficient lossy compression of sampled signals followed by reconstruction. The objective is to reconstruct a predesignated subset of signals with a specified level of accuracy. Processing of the signals must be universal in that the combined sampling, learning and compression must be robust in the face of inexact prior knowledge of the underlying probability distribution of the signals. Rooted in information theory, this research project also explores innate connections to joint probability distribution learning (in statistical learning theory) and correlated multi-armed bandits (in machine learning).

The larger goal of the project is to understand connections among universal spatial sampling, distribution learning and compression rate-distortion performance. Furthermore, it aims to create advances in information theory through the introduction of new models and concepts, and in probability distribution learning and machine learning through new formulations and solutions. Expected outcomes are new techniques for joint distribution learning; and a characterization of fundamental performance limits and the structure of optimal universal sampling and compression that will guide algorithm design.

Published July 19, 2019